1の位が0でない3けたの自然数がある。この数と,百の位と一の位を入れ替えて出来る数との差は99の倍数である。このわけを,文字を使って説明しなさい。 スポンサードリンク 例えば たとえば752の場合,百の位と一の位を入れ替えると257になりますので, スポンサードリンク =495注意1:添字は,「0」 から 「要素数 1」 の範囲. この範囲外の要素を参照しようとすると,プログラムが不正終了する(しない場合もある). 注意2:一般の変数と同じく,配列も宣言しただけでは中身は不定(=ゴミが入っている). 配列の添字には,変数も使うことができる(これがPython 31 からは、ほとんどの場面で 01 のような最も短い桁数の10進数の値を選ぶようになりました。 この動作は2進数の浮動小数点にとってはごく自然なものです。これは Python のバグではありませんし、あなたのコードのバグでもありません。
中学数学文字式の利用3けたの正の整数で 100の位 十の位 一の Yahoo 知恵袋
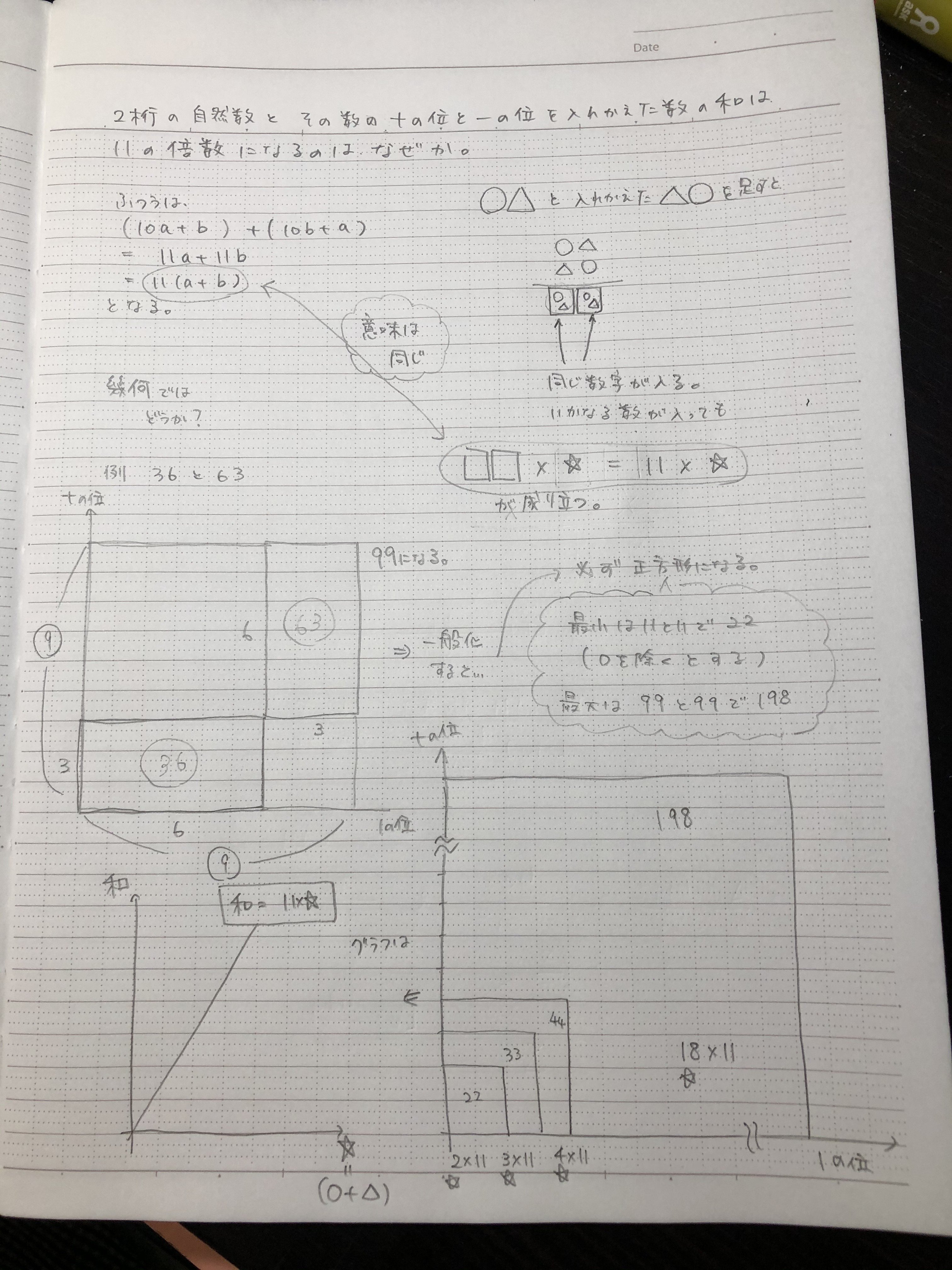
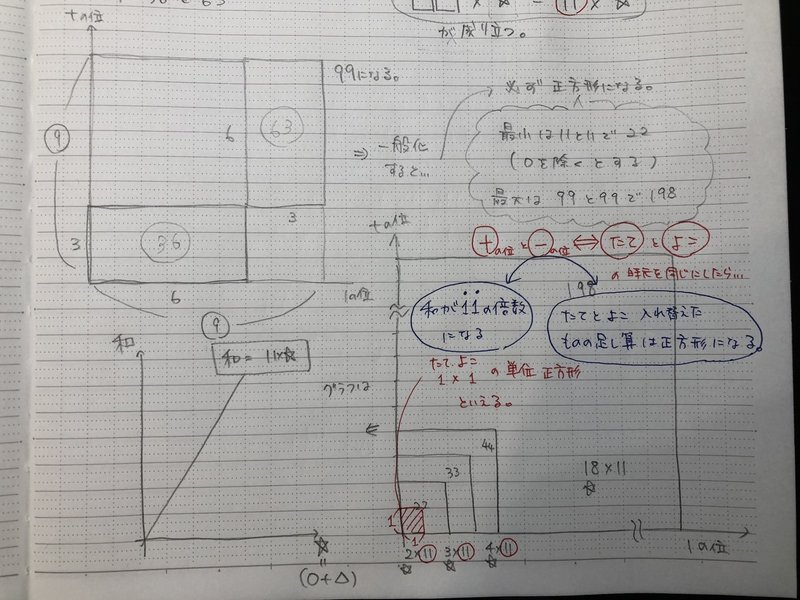
2桁の自然数とその自然数の1の位の数と十の位の数を入れ替えた数の和は11の倍数になります このことを文字を使って説明しなさい
2桁の自然数とその自然数の1の位の数と十の位の数を入れ替えた数の和は11の倍数になります このことを文字を使って説明しなさい-About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators56の十の位の数は5, 一の位の数は6である。 この5, 6を使って56という数字を表すと 56 = 50 6 = 5×10 6 となる。 つまり (2けたの自然数)=(十の位の数)×10(一の位の数) 一の位の数と十の位の数との和が12となる2けたの自然数がある。この自然数の十の位と一の位の数を入れ替えた数はもとの数よ



数学でわからない問題です 3桁の正の整数がある この整数の十の位の数は4 各位 Yahoo 知恵袋
FC2 is nalyzer services and others Our blog service is ranked No2 domestically and supported by wide range of users including both beginners and heavy users We offer as many as 30 different services例2 2けたの自然数Pがある。Pの十の位の数と一の位の数を入れ替えた数をQとする。 PQが9の倍数になることを説明せよ。 文字で表す 十の位の数をx, 一の位の数をyとすると2けたの自然数Pは10xyとなる。 また、十の位の数と一の位の数を入れ替えた数Qは10yxと(RAND関数で返される値は小数値になっていることを示すためです。) この方法では、1~10の乱数が表示できましたが、同じ値「2」が3個あり、「6」が2個あり、「1」や「4」がありません。 1~10の整数値をA1A10にランダムに1個ずつ表示するには? topへ
Abが11の倍数となることを説明しなさい。 3 3けたの自然数aがある。aの百の位の数と一の位の数を入れ替えた自然数をbとする。abが99の倍数になることを説明しなさい。 4 2けたの自然数から、この2けたの自然数の十の位の数と一の位の数の和を引くと9の倍数になる。これを説明しなさい。 5整数の問題なんですが・・ 1335 回答を見てもピンときません・・・ (問題) 2桁の自然数があります。 十の位の数字と一の位の数字を入れ替えた数から元の数をひくと正になり、かつその結果が27の倍数になります。 このような自然数は何個「2つの自然数がともに奇数であるとき、それらの和は偶数になる」ことの説明の仕方 2つの奇数を各々 2m−1, 2n−1 とおく。( m, n は自然数)← (3) (3)の字面にこだわって 2n−1, 2n−1 とおいてはいけない。このようにおくと、2つの奇数が同じという仮定を勝手に持ち込んでしまうことになる
3桁の自然数の各、位の数の和が3の倍数ならば、その自然数は3の倍数である。 っていう問題の証明がわかりません。教えて下さい。 0 この回答がベストアンサーに選ばれました。 ぽんすけ 3年以上前 こんな感じです。 0 チョコ( ´ ` )ノ 3年以上前 なるほど〜。やっぱり、3の倍数自体の証明この教材では行列式を(*1)(*2)のように定める上記の 1,2,3 などの性質が成り立つことを示し,これを使って行列式を変形する方法を学ぶ. 以下,具体的に示すために3次の行列式の場合を例として示すが,他の場合でも同様に示せる.MINVERSE 関数は、配列に格納されている行列 2ケタの正の整数と、その数の十の位をbと一の位の数を入れ替えてできる数との和は11の倍数になります。 上の問題で考えた2数の和について、11の倍数であること以外にどんなことがわかりますか? という問題なのですがわかる人お願いします 中学数学 文章題です。十の位と一の位の数の和




不思議数との出会いの覚え書き50篇




文字式を使った整数の証明 数学解説ブログ つくば市の 数学 算数 物理に強い プロ家庭教師 長通幸大 発信
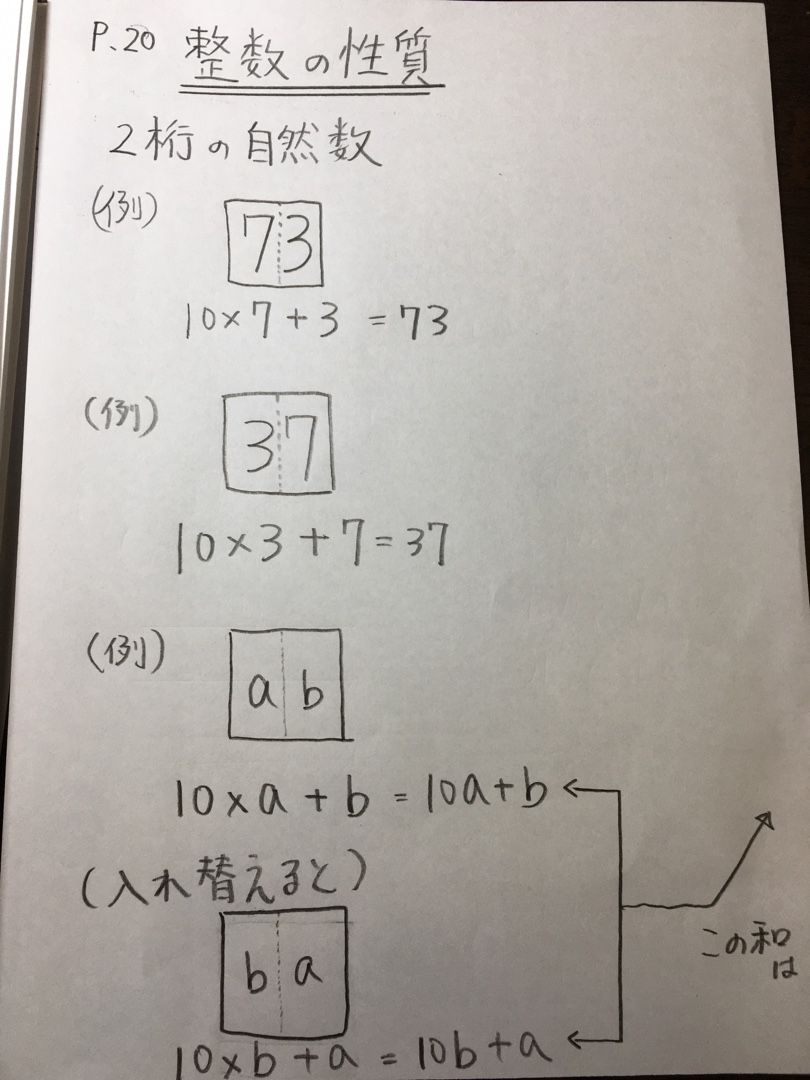
中学の数学の問題で、 一のの位の数が0でない2桁の自然数と、その一のフライの数字と十の位の数字を入れ替えた数との和は11の倍数になる。この理由を説明しなさい。 という問題があり、その本にある説明が、 (10ab) (10ba) = 10ab10ba = 11a11b = 11(ab) (a,bは02桁の自然数と,その数の十の位の数と一の位の数を入れ替えた数との和は11の倍数になります。そのわけを説明しなさい。 解説・解法 問題が少しややこしいし読みづらいかもしれません。問題を具体化していくと,たとえば 「2桁の自然数」を25とすると(4) 連続する2つの奇数の和は4の倍数であることを文字を用いて説明してください。 (5) 2けたの自然数と、その数の一の位の数字と十の位の数字を入れかえた数の和が11の倍数になることを文字を使って説明してください。




中学生のための中学数学の質問掲示板



学習指示 中2 数学 整数の性質 応用p P22 超重要ページ 坂東市進学塾 スタディ ポート 港日記 楽天ブログ
2 けたの自然数を,十の位の数字を a,一の位の数字を b として, a, b を使って表せ。 解答欄 解答 10a b 解説 例えば,2 けたの整数 56 は,56 50= 10×5 6 と表すこ とができる。十の位が a ,一の位が b の2 けたの整数は, 10×a b = 10a b と表すことができる。同様にして,百の位 が a ,十 数学・算数 中2 式の計算 説明問題についてです。 何問か解けないのでお願いします。 (1)十の位の数が0でない3桁の自然数がある。この自然数の百の位の数と、一の位の数を入れかえた3桁の自然数を 質問No 数学・算数 ある2ケタの自然数がある・・・ ある2ケタの自然数がある。十の位の数字と一の位の数字を入れかえた数を作り、もとの数を足すと、11の倍数になることを説明しなさい。 これの解答の仕方がわ 質問No



7の倍数判定法 数学カフェjr




中学2 3年生 数学 式による説明のコツ 例題集と模範解答例 こんな問題が出題される
中学の数学の問題で、 一のの位の数が0でない2桁の自然数と、その一のフライの数字と十の位の数字を入れ替えた数との和は11の倍数になる。この理由を説明しなさい。 という問題があり、その本にある説明が、 (10ab) (10ba) = 10ab10ba = 11a11b = 11(ab) (a,bは0この説明では0、00は考慮していないんだけれどね。う~ん 252 名前:132人目の素数さん投稿日: 1345 >251 なるほど。でもこの問題難しいな。 253 名前:132人目の素数さん投稿日: 1903 00枚のカードが積んである。上から順に1,2,3、、、00と番号が書いてある。 一番上のカードを下 この問題あっていますか? 写真見えにくかったらごめんなさい。 問題はまるで囲ってるところです〇 10YX と表される。 X+Yは整数だから9(X+Y)は9の倍数である。 したがって2桁の自然数とその数の1の位の数字と10の位の数を入れ替えた数の和は9の



Sonoda Jimdo Com



2
Xに負数や複素数が入力できます。 例 ln(23i)= i お客様の声 アンケート投稿 よくある質問 リンク方法 対数関数 110 /96件 表示件数 1 43 40歳代 / エンジニア / 役に立った / 使用目的 使用bit数の計算 2 1227 歳未満 / 高校・専門・大学生・大学院生今回は簡単なその使い方をご紹介します。 Rnd関数の使い方 Rnd関数は、0以上1未満の乱数を返します。構文は下記です。 crayo 17/3/3更新 Excel VBAで範囲を指定して乱数を生成する:Rnd,Int 6 タイトルとURLをコピー Excelの作業で切っても切り離せない乱数ですが、VBAでは、Rnd関数を使の させ ん Level B 101 次のことが成り立つわけを, 文字を用いて説明しなさい。十 ム 図(1) 2けたの自然数について,各位の数の和が3の倍数ならば, この自然数は3の倍数 である。 生ちの 円半すさ強面 8 d yk ×x t の円半008す ラ予 9A 土最の歴の円半さを A 3る




これって計算どうしますか Clearnote



2
2ケタの自然数と、その数の1の位と10の位の数字を入れ替えた数の和は11の倍数になることを文字を使って説明しなさい っていう問題が 出たのですが だれか教えてください。分りやすくお実際の暦体系では不定期に付与されるうるう秒 # は考慮しなくて良いものとする正しい日付でない場合はその旨出力し処理を中止する 二つの時刻の時間差を表示する 準グレゴリオ暦入力(_準グレゴリオ暦1,_年1,_月1,_日1,_時1,_分1,_秒1), 準グレゴリオ暦入力(_準グレゴリオ暦2,_年2,_月2,_日2,_時2




世界一わかりやすい数学問題集中2 1章 式の計算




板橋区立板橋第二中学校




中学数学 中2文字式を使った説明 数樂管理人のブログ



2




詳しく解説お願いします Clearnote



2



位の数 を入れ替えた2桁の自然数 数学カフェjr



数学でわからない問題です 3桁の正の整数がある この整数の十の位の数は4 各位 Yahoo 知恵袋




この問題あっていますか 写真見えにくかったらごめんなさい 問題はま 中学校 教えて Goo




2桁の自然数があり 十の位と一の位は共に偶数か共に奇数である この数の十の位 Clearnote



2




中学数学 1次方程式 文章題の解き方 整数 自然数



2




2 13の倍数の判定法をまとめ 簡単な倍数の見分け方




中学数学 1次方程式 文章題の解き方 整数 自然数



2




中学数学 1次方程式 文章題の解き方 整数 自然数



2




99以上 1 から 100 まで の 100 枚 の 番号 札 から 1 枚 引く とき 4 の 倍数 または 7 の 倍数 が 出る 確率 シモネタ




台東区立忍岡中学校




中2数学 文字式の利用 後藤塾ブログ



証明の問題2ケタの自然数と その数の一の位の数字と十の位の数字を入 Yahoo 知恵袋




中学2年の数学 動画 文字式の利用 2けたの自然数編の問題 19ch



2



2



2




連立方程式文章題 2けたの自然数



2




連続投稿すみません 人 分かりません A Clearnote



3




北辰 期末 中2数学 文字と式 蒼進塾 そうしんじゅく さいたま市 真剣に努力する姿勢を育む




数的推理 倍数 約数問題の解答解説してみた 過去問 いい仕事 みつけた



一の位が0でない2ケタの自然数と その自然数の一の位の数と十の位 Yahoo 知恵袋




中2数学 文字式の利用の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



2



2




北辰 期末 中2数学 文字と式 蒼進塾 そうしんじゅく さいたま市 真剣に努力する姿勢を育む




文字式による証明 十の位と一の位 Youtube




これって計算どうしますか Clearnote



2




体育館のネット完成 5月 21年 江西中学校 ブログ 江西中学校



2



2ケタの正の整数と その数の十の位をbと一の位の数を入れ替えてでき Yahoo 知恵袋




ベスト中 2 数学 式 による 説明 最高のカラーリングのアイデア



3



2けたの正の整数があって この整数の一の位の数と十の位の数を入 Yahoo 知恵袋




中学2年生数学1学期期末テスト予想問題と解答 解説 Pikuu




10の位がx 1の位がy の二桁の自然数 Youtube



中学校数学




数学 中2 25 連立方程式の利用 数編 Youtube




3方程式の文章問題 十の位と一の位の数を入れかえ Youtube




文字と式 第三章 式と計算 とある研究員の妄想伽話



2



3桁の自然数 3 19西大和学園 数学カフェjr




3桁の自然数の中で 次の個数を求めよ という問題なのですが 以下の 数学 教えて Goo




2桁の自然数に関する説明2 中学数学 講義 Youtube




過去問 21 令和3 年 都立新宿高校 数学 前編 大問1 2 高校受験のための数学



2




中2数学 2ケタの自然数 の表し方 練習編 映像授業のtry It トライイット



2



Nier Go Jp



2



Nier Go Jp



整数の性質の説明3 チーム エン



2



二桁の整数があります この数は各桁の数の和よりも27大きく 10の位と1 Yahoo 知恵袋




台東区立忍岡中学校




体育館のネット完成 5月 21年 江西中学校 ブログ 江西中学校




動画授業のページ 進学塾ブリッジ




かけ算の順序 なんてもう古い 今や時代は 足し算の順序 Togetter



1



2




十の位の数字と一の位の数字の和が9である2けたの整数は9の倍数である このこ Clearnote



2




問1の考え方を教えてください Clearnote



1




数学 中2 11 文字式の利用 2けたの自然数編 Youtube



2



中学数学文字式の利用3けたの正の整数で 100の位 十の位 一の Yahoo 知恵袋



2




無料プリント こだま学び舎プロジェクト



2けたの正の整数がある この整数の一の位の数を8倍し 十の位の数を加えると2 Yahoo 知恵袋




体育館のネット完成 5月 21年 江西中学校 ブログ 江西中学校




中学数学 1次方程式 文章題の解き方 整数 自然数




中学数学 文字と式 中2 文字式の利用 整数の性質 2ケタの自然数 Youtube



二桁の自然数とその数の十の位と一の位入れ替えた数の和 Tatsu Note




体育館のネット完成 5月 21年 江西中学校 ブログ 江西中学校




Laf 中学生のオンライン学習塾 Posty Facebook



2




高校数学a 余りが一致する条件 2乗しても下2桁が変わらない自然数 受験の月



Izumi Math Jp



二桁の自然数とその数の十の位と一の位入れ替えた数の和 Tatsu Note




体育館のネット完成 5月 21年 江西中学校 ブログ 江西中学校



十の位 一の位を入れかえてできる数 苦手な数学を簡単に



0 件のコメント:
コメントを投稿